oooops! my fault

It's not a unit step function. If it was, the output would asymptotically reach a constant value. This would be the analogue of an infinite supply of oil.
It´s possible to conclude that when you look for a circuit that started with zero energy, and the graph shows that in some point in the future it will return to zero, it was obviously stimulated by something that started in zero and will end in zero energy, like a decaying pulse that instantly jumps from zero to some constant and decays back to zero at infinity.
by considering the unit step function, i´ve just integrated my interpretation, because when i look at energy consumption, i like to watch and account the total accumulated energy consumed.
your idea of creating a physical electrical model to do some analogy to whats going on in the "macroscopic" level is a fantastic tool for doing some predictions, let´s discuss a few improvements, because when it starts to improve, the graphs obtained in the linearization process, if the model is well calibrated, should reflect exactly the real life graphs, which is good, because is gives ahead information sharing for us, here at peakoil.
IMO i think that is better to create a model on the integration side and watch for the zero and first derivative graphs, instead of looking only at the derivative side and integrating the results.
this will be surely is more difficult but the precision of the results are worth the work involved.
IMO the initial idea is to conceive a circuit that starts with C1 (which can be zero or not) initial energy and by the flip of a switch it jumps to C1+K level of energy.
the behaviour of this circuit (which i have no clue on how to make) at the input will be obviously a step function, but the objective at the output is to obtain a logistic simmetrical step output at D0 and a hubbert curve at D1.
now that the purpose of this black box is know, what are some useful parameters to it? how many of them?
now comes a very interesting part, which is to conceive an "eroei" stage.(which i have much less clue than the first stage)
the eroei stage states that if you supply a hubbert curve on the input side, the result on the output stage is a mirrored capacitor discharge curve like the one that appears in your first line of graph of in the net energy my net energy graph (already mirrored).
if you reflect for some time about this, then you can ask yourself.
how is it possible to conceive a circuit that behaves exactly like a mirrored capacitor charge discharge graph? especially when this graph appears as the result of the input of an exponential decay pulse?
because, at a first glance, to obtain the mirror for this graph would mean to assume "negative" linear time, which is not possible right? this is aparently the only way to mirror this curve....
i´ll leave a few private conclusions for the next post, to allow some reflection on this puzzle, but i´m curious to know what are your ideas on how to deal with the implementation of a circuit for this task.

Put simply, volume of discoveries = volume of production. The stages in between can be thought as virtual volumes that we never see in the abstract sense
do you mean by this, that all the areas under the curves of all stages are the same?

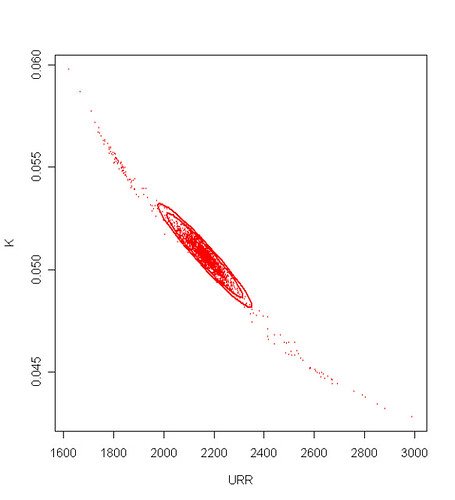
 ) has a bootstrap library called 'boot' that implements almost all the standard techniques. I won't go into the details of the Bootstrap theory, a lot of details about the techniques and the R language implementation used in this post can be found in the following document:
) has a bootstrap library called 'boot' that implements almost all the standard techniques. I won't go into the details of the Bootstrap theory, a lot of details about the techniques and the R language implementation used in this post can be found in the following document:









 [/align]
[/align]
 [/align]
[/align] [/align]
[/align]
 [/align]
[/align]