WebHubbleTelescope wrote:I checked on the Ricatti. It looks like you did an excellent job reproducing the math in some of your supporting posts. Weird how the URR seems really low (~1600) which causes the curve to do a nose-dive between 2010-2030. However, if you push up the URR to 2500, the curve flips upward crazily. You said something about adding another control function to suppress this, but this non-linear stuff sometimes has a mind of its own.
I agree, the shock function is hard to handle and is poorly justified by Guseo. Guseo finds an URR around 1,600 Gb and he claims that his approach does not require prior knowledge of the true URR value. It's not entirely true because I found that the final result for the URR will strongly depend on the choosen initial value - which reflects what you think the URR should be! - as you can see on the graph.
WebHubbleTelescope wrote:I don't have any non-linearities in my formulation apart from the forcing function (which relates to the discovery curve). This makes it well-behaved for all parameter inputs, so that you don't get those unexpected swings.
I have to find time to seriously go through your work at mobjectivist.com.
Thanks for the reference!rockdoc123 wrote: there is a really good reference book out there
Decision Analysis for Petroleum Exploration, 1975, Newendorp, Planning Press, Colorado, 668 pp.
This is a classic study in Bayesian logic applied to oil and gas problems, the chapter titled "Probabilities of Outcomes of Multiwell Drilling Programs" addresses some of the issues you probably need to think about when simulating..starts on page 327.
SilentE wrote:That means that a single WHT-Hubbert curve will only fit in a constant-price domain. It follows that the linearized derivative of the WH curve will also only give you a straight line to an accurate URR in a constant-price domain. When prices shift, URR shifts too! But that's sort of obvious: if you are estimating URR based on past production only in a constant-price domain, you are making the assumption that prices will not change. If prices change, more oil becomes "economical" to produce, so URR increases.
Guseo tried to build a price-based shock function but with not much success! one piece is missing here, you will have to model demand in order to infer the impact of high prices. If demand is strong, the probability of higher prices increases which creates an economical incentive to explore more and to implement thrid/fourth generation EOR techniques. But EOR is not applicable on all fields and will have not the same success on all fields. Projected Increased in URR are mainly projected oil displacement from the P50 reserves to the P90 prior to any real implementation.
EnergySpin wrote: (and by the way , most librarians think that I'm crazy when they realize that a MD is poking into the geology section of the library Rolling Eyes)

EnergySpin wrote:B) Modelling oil reservoir discovery = EXPLORATION. I found particularly enlightening the comments that rockdock made about log-normal distributions. Are these the terms "creaming curves" are understood? If we had access to discovery data we could estimate such distributions from start by using non-parametric kernel based methods and not rely on fixed parametric assumptions
Agreed. It seems to work. I stumbled on an article of Laherrere on that matter.
EnergySpin wrote:A) Modelling of the physical processes that describe indivindual well behaviour.
We need to define what level of granularity (oil field or wells) is really necessary being careful to to go too low because reservoir modeling is a very very complex science! WHT used rather simple models which gave reasonnable results.
me neither! this is quite a difficult problem. I`m not aware of any research paper on that issue.EnergySpin wrote:C) Modelling the economy i.e. supply and demand . My understanding is that markets are modelled using Stochastic Differential Equations (e.g. Black Sholes formula), but I have absolutely no technical experience in either deploying these mathematical tools (although I'm a fast learner!) or even understand the econometrical context ... Any volunteers?
EnergySpin wrote:For that I propose we use the open source R (http://www.R-project.org) and (win)BUGS from http://www.mrc-bsu.cam.ac.uk/bugs/welcome.shtml
The second can be dowloaded for free after registration .... and there is also a library that allows R and BUGS to communicate. This will at least guarantee a conformity of tools .... and allow people to test predictions/assumptions on their computers.
However such tools require data, data, data (old and new) and here I rest my case . I hope that other people may contribute ...
I agree, I've already started my learning curve on the R language.
EnergySpin wrote:F) Getting the data: rockdock/shakespear1/taskforce_unity any ideas?
I think it should be the first step. Collect the different data and build a data repository which can be easily consulted and updated.

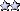

 ) gives the general solution:
) gives the general solution:
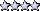
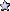



 )
)