[khebab]

Let me know if tables, graphs, source-code spreads, etc. need formatted display here. There might be a couple options in phpBB that allow things we haven't tried before.

thanks for asking! formatted display for tables and source-code spreads could be interesting.

[khebab]

I've seen a couple of mentions that field size has a Zipf distribution. FWIW...

I think it is pretty well agreed amoungst the folks who make a living at this (Pete Rose and Robert Megill come to mind) that field size distributions are fairly well described by a lognormal distribution. The thought being that anything that is a net result of multiplication of a number of random variables will result in an approximate lognormal distribution. Given all the other uncertainties probably not a bad approach.

I finally found some info in Simmons's book in the appendix B (p. 374 and 375):

Code: Select all

[i]volume and production in mb and mbpd[/i]
Field Size         No of   Tot.
(production vol.)  fields  Prod   <1950  50s  60s 70s 80s 90s
1,000+             4        8,000   2    1    0   1   0   0
500-1,000         10        5,900   2    3    3   1   1   0
300-500           12        4,100   3    1    6   1   1   0
200-300           29        6,450   8    4    6   9   1   1
100-200           61        7,900   5    8    13  13  11  11
0-100           4,000+      36,200  ?    ?    ?   ?   ?   ?
Total           4,061+      38,550  ?    ?    ?   ?   ?   ?


the last line is taken from Figure B.1 p. 374 but there are no information on the time of discovery distribution. The production figures are for 2000.

[khebab]

Here the corresponding bar chart (without the small fields):


Figure 8

[WebHubbleTelescope]

EnergySpin
I agree with your comment regarding the need to look at this with a stochastic view. I've actually played around with simpler models than Khebab used here...generally just for one or two pools. My assumptions are more general (assume peak production after 1 year ramp up...peak at 10% of URR...held for 2 - 5 years depending on field size and then declined at 10% /annum) but are what we normally use as first approximations. Usually I put in lognormal distributions for reserves and other assumptions regarding production/depletion. I've been using Crystal Ball in Excel but also have @Risk on my laptop. Pup55 sent me his Saudi depletion profile in excel format quite awhile ago and I have been meaning to fiddle around with that in Crystal Ball...unfortunately there are more things I would like to do than I have time for.
To my mind this whole discussion around Peak Oil could benefit greatly from discussing both reserves and production/depletion and demand from a stochastic viewpoint.

We all wished we had more time; PO is rather expensive hobby as far as time is concerned.
I did give Verhulst/logistic modelling a shot a while back in this forum and I was appaled. This is a nasty curve to fit data to; I'm not surprised that most predictions have been wrong. ....

I appreciate your take and expertise on data regression. But like Rockdoc, I have heartburn with the logistic model for more fundamental reasons. Why should it work at all for this class of behaviors? When did the strong non-linear component of the basic "predator/prey" get applied to oil depletion?

I have been playing around a lot with the stochastic formulation staying away from the non-linear terms, apart from the forcing function which corresponds to newly tapped discoveries.

Symmetric Triangular discovery window


Welch (upside down parabola) discovery window -- "logistic"-like


Khebab has got some curves with some of the same characteristics, but again, I just do not like the fact that we are solving the Verhulst equation to provide the parametric fits.

I have time to work this out some more. I have a post up where I list the posts I have done in the last few months.

http://mobjectivist.blogspot.com/2005/1 ... posts.html

Recently, I have tried to account for the oil shocks and even more recently have tried to understand the mathematical and physical underpinnings of the logistic curve model. Like I said, a bit frustrating that last bit. On the other hand, a stochastic model works brilliantly to account for oil shocks, i.e. the dips in the production curves.

[SilentE]

Khebab opened a can of worms .... it will be interesting as hell
....
Maybe it is time to turn this into a real community project.

I'm looking forward to reading about it.

One suggestion: if you present results, make sure you specify what type of numbers you're using: conventional only, "all liquids", future non-conventional, which types, etc...

=====

I've commented in a couple of places about WHT's efforts - good stuff no doubt. (@TOD and Mobjectivist) I think WHT is totally right that relying on unsupported logistic models is VERY bad for PO.

I'll confess that I was initially interested in PO because I saw the numbers and the Hubbert analysis - and the Scientific American article. I read about Simmon's new book and his concerns about the Saudis. I assumed there was a sound mathematical economic or geologic model under it that led to the imminent PO conclusions. I went to find out more...

Note to the unwary: under NO circumstances should you confuse friend-of-the-White-House Matt Simmons with LATOC-paranoid Matt Savinar.

When I found out there really wasn't much of a model, I was a little dismayed. I expected a bunch of folks calling themselves "Environmental Economists" (e.g., Heinberg) to actually engage in some economics: price effects, elasticities, market behavior models, etc. I expected the geologists to have a bit more understanding of economics. Moreover, every time I tried to find something related to the subject, I'd find something that suggested that price was VERY important and that the PO folks were flat out wrong about a LOT of things...

So, in short, I think this is a great effort.

- Silent E, aka "Eroei van Tanstaafl" @ TOD

[SilentE]

I finally found some info in Simmons's book in the appendix B (p. 374 and 375):

Code: Select all

[i]volume and production in mb and mbpd[/i]
Field Size         No of   Tot.
(production vol.)  fields  Prod   <1950  50s  60s 70s 80s 90s
1,000+             4        8,000   2    1    0   1   0   0
500-1,000         10        5,900   2    3    3   1   1   0
300-500           12        4,100   3    1    6   1   1   0
200-300           29        6,450   8    4    6   9   1   1
100-200           61        7,900   5    8    13  13  11  11
0-100           4,000+      36,200  ?    ?    ?   ?   ?   ?
Total             61        32,350  20   17   28  25  14  12


the last line is taken from Figure B.1 p. 374 but there are no information on the time of discovery distribution. The production figures are for 2000.

It looks like the last two lines are mucked up. The "total" production of 32,350 is actually a sum for the fields of size 100-1000+. It obviously does not include the larger number for fields size 0-100. Also, the "total" No. of Fields is 61 - but this is the same as the number of fields size 100-200. The total for 200-1000+ is 55, so if this "total" actually excludes the 0-100 size, it should still be 116. But the table could be incorrect in other ways as well (or instead).

Q1: what if you model future discoveries in the 100-300 range? Looks like there should be perhaps another 200-300 and perhaps 30+ more 100-200 size fields? We could compare to the 2000-2005 period to check the model?

Q2: what about discoveries under 100? They are more than half of the production, if the 36K is correct. We should expect that a growing percentage of production will come from the smaller fields in the future. What does that imply for a production forecast that ignores smaller fields?

[Taskforce_Unity]

Here's some thoughts from someone who doesn't understand half the words in this thread .

Are you guys intending to do a special statistical method for calculating the production increase and subsequent decline of fields with EOR techniques and waterflooding (based on fields that show this trend?)

If you need a data gatherer i am willing to spend some hours looking for production data.

[khebab]

One suggestion: if you present results, make sure you specify what type of numbers you're using: conventional only, "all liquids", future non-conventional, which types, etc...

Good suggestion, unfortunately available data on the web is not always that clear.

I've commented in a couple of places about WHT's efforts - good stuff no doubt. (@TOD and Mobjectivist) I think WHT is totally right that relying on unsupported logistic models is VERY bad for PO.

The logisitc is more an historical model and not a state of the art approach. Parameteric methods are usually the first think you try on a new problem because they are easy and quick (even Excel does it now). A lot of posters (WHT, EnergySpin, etc.) have many skills in advanced statistical techniques. Why not using this potential? I intend to put the code in an Open Source framework (R software) so that anybody can experiment and improve it!

Moreover, every time I tried to find something related to the subject, I'd find something that suggested that price was VERY important and that the PO folks were flat out wrong about a LOT of things...

That's the big challenge! how to include price fluctuations in a depletion model! the first to have proposed something is Guseo with the GBM model (Peak prediction based on the Riccati equation: 2007!).

It looks like the last two lines are mucked up. The "total" production of 32,350 is actually a sum for the fields of size 100-1000+. It obviously does not include the larger number for fields size 0-100. Also, the "total" No. of Fields is 61 - but this is the same as the number of fields size 100-200. The total for 200-1000+ is 55, so if this "total" actually excludes the 0-100 size, it should still be 116. But the table could be incorrect in other ways as well (or instead).

It's my mistake, the original table from Simmons does not include the small fields (0 to 0.1 mbpd). I took it from another graph in his book (Figure B.1). Unfortunately, it does not give the distribution of discovery per decades.

Q1: what if you model future discoveries in the 100-300 range? Looks like there should be perhaps another 200-300 and perhaps 30+ more 100-200 size fields? We could compare to the 2000-2005 period to check the model?

This class of field is rather broad but I have no data to make it more refiend. In order to project future discoveries, I just took the last distribution of field size (for the 90s) and assumed that it was similar for the years 2000s and 2010s.

Q2: what about discoveries under 100? They are more than half of the production, if the 36K is correct. We should expect that a growing percentage of production will come from the smaller fields in the future. What does that imply for a production forecast that ignores smaller fields?

VERY GOOD QUESTION! I have no data on the distribution of the discovery for small fields (0-100 tbpd). Simmons is just saying that there are 4,000+ fields that have been discovered up to the year 2000 which are providing 53% of the world production!. That'it, that's all! In statistics, when we have no knowledge, you usually assume a uniform distribution which gives about 700 discoveries per decades. However, since discoveries have been declining since the 80s I assumed a uniform loss of 100 new fields per decades.

Code: Select all

[i]volume and production in mb and mbpd[/i]
Field Size         No of   Tot.                               | Extrapolation
(production vol.)  fields  Prod   <1950  50s  60s 70s 80s 90s 2000s 2010s
1,000+             4        8,000   2    1    0   1   0   0     0     0
500-1,000         10        5,900   2    3    3   1   1   0     0     0
300-500           12        4,100   3    1    6   1   1   0     0     0
200-300           31        6,450   8    4    6   9   1   1     1     1
100-200           83        7,900   5    8    13  13  11  11    11    11
0-100           4,400      36,200  900  800  700 600 500 400   300   200
Total           4,540      38,550  920  817  728 625 514 412   312   212


Are you guys intending to do a special statistical method for calculating the production increase and subsequent decline of fields with EOR techniques and waterflooding (based on fields that show this trend?)

I'm thinking about it, but it's rather complex to model because it's a nonlinear behavior. Probably, some EOR techniques were not available before the 80s. I was thinking about adding a kind of shock function that could boost production past the peak.

If you need a data gatherer i am willing to spend some hours looking for production data.

YES, I need data! in particular on small fields (0-100 tbpd) which constitute the majority of the world production.

[WebHubbleTelescope]

That's the big challenge! how to include price fluctuations in a depletion model! the first to have proposed something is Guseo with the GBM model (Peak prediction based on the Riccati equation: 2007!).

Khebab,
I checked on the Ricatti. It looks like you did an excellent job reproducing the math in some of your supporting posts. Weird how the URR seems really low (~1600) which causes the curve to do a nose-dive between 2010-2030. However, if you push up the URR to 2500, the curve flips upward crazily. You said something about adding another control function to suppress this, but this non-linear stuff sometimes has a mind of its own.



I don't have any non-linearities in my formulation apart from the forcing function (which relates to the discovery curve). This makes it well-behaved for all parameter inputs, so that you don't get those unexpected swings.

[pup55]

the 4039 curve (red line) is a plausible scenario if you believe the US-EIA and others who predict demand will continue to grow at a current rate, and we have the reserves to pump.

But, do you really want to be around between 2030 and 2040? The backside of this curve will be really painful.

[pup55]

usually assume a uniform distribution which gives about 700 discoveries per decades

I've been dreaming about a little simulator on this, sort of like the game "battleship", which the north americans might be familiar with.

You have a "base field" of a given area, and a distribution of oil deposits of various sizes within the field.

You randomly drill X number of holes per year into the field. If the hole hits an oil field, it is discovered. If not, it is a dry hole. The ratio of the area of the base field to the area of possible oil fields is such that it gives the approximate ratio of dry holes to successful strikes that we have historically seen.

You set up the oil deposits so as to have the same distribution as the real oil deposits: super giants, giants, smaller and smaller per the distribution above. Lots of little ones, evidently.

You should be able to test various assumptions: probability of a strike given the drilling of X number of holes, increasing or decreasing the number of holes drilled per year (or decade) so as to give various discovery curves. You should be able to compute statistically the probability of striking an additional super-giant after a certain number of years, given increases or decreases in the number of holes drilled, etc.

Since we have historical rig counts, etc. should be no problem to set up parameters that more or less mimic what happened historically. From then, you can start to predict the future.

At least you would be able to estimate, with a known confidence interval, how many holes you will have to drill in order to increase discoveries by X amount, knowing as we do that it has been a long time since the last giants and supergiants have been discovered and there is likely mostly little deposits left to discover.

Anyway, this is my daydream at the moment. I have not figured out how to program it yet.

[rockdoc123]

Pup55...this is a worthwhile endeavour. One of the challenges is that you need to treat exploration risk in any given basin as semi-dependant (your first discovery will lower the risk on subsequent discoveries) and between basins as independant. Rather than go into a huge discussion on probability and bore everyone with the formulas there is a really good reference book out there
Decision Analysis for Petroleum Exploration, 1975, Newendorp, Planning Press, Colorado, 668 pp.
This is a classic study in Bayesian logic applied to oil and gas problems, the chapter titled "Probabilities of Outcomes of Multiwell Drilling Programs" addresses some of the issues you probably need to think about when simulating..starts on page 327.
If memory serves me correctly IHS as information on statistical success rates in various basins which might also be useful as a model.

[SilentE]

That's the big challenge! how to include price fluctuations in a depletion model! the first to have proposed something is Guseo with the GBM model (Peak prediction based on the Riccati equation: 2007!).

Hmmm.... (after reading paper and thread) it looks like that model isn't so sweet. I'm not sure why they wanted a base model that decellerates so sharply. It just doesn't pass my smell test - and judging by the comments, I'm not the only one. Note that their model would have trouble trying to model post-peak US production because of the long shallow tail - and that in an environment where price-feedbacks are suppressed due to cheap imports!

Q2: what about discoveries under 100? They are more than half of the production, if the 36K is correct. We should expect that a growing percentage of production will come from the smaller fields in the future. What does that imply for a production forecast that ignores smaller fields?

VERY GOOD QUESTION! I have no data on the distribution of the discovery for small fields (0-100 tbpd). Simmons is just saying that there are 4,000+ fields that have been discovered up to the year 2000 which are providing 53% of the world production!. That'it, that's all! In statistics, when we have no knowledge, you usually assume a uniform distribution which gives about 700 discoveries per decades. However, since discoveries have been declining since the 80s I assumed a uniform loss of 100 new fields per decades.

Hmmm... we definitely need more data.

[SilentE]

WHT's work at Mobjectivist offers a constant-price Hubbert model, but derived from something other than the logistic model. It shows that although Hubbert got the mathematical basis for the curve wrong, he was right about the shape and its implications. And in the constant price environment of 1955-1970, Hubbert was near-dead on.

Although there were important external political factors that Hubbert could not predict (e.g., the Tex RR Comm), it seems to me that those factors were operating to Hubbert's benefit because they were operating to maintain a constant price. Hubbert's luck originates from the fact that the constant-price environment his theory required (an assumption of which he was unaware) persisted because of political interference until his peak prediction occured.

That means that a single WHT-Hubbert curve will only fit in a constant-price domain. It follows that the linearized derivative of the WH curve will also only give you a straight line to an accurate URR in a constant-price domain. When prices shift, URR shifts too! But that's sort of obvious: if you are estimating URR based on past production only in a constant-price domain, you are making the assumption that prices will not change. If prices change, more oil becomes "economical" to produce, so URR increases.

We can check this by examining a second period of roughly constant real prices: 1986-2000. Did production follow your curve? If so, then we can perhaps estimate part of the relationship - we know the factor by which prices rose, so perhaps we could link price increases to shifts in the curve?

It'll have to boil down to price elasticities of demand, both short and long term, and price elasticities of supply - new discoveries or "reserve growth". There's also going to be a technology factor, but from what I've seen it would be small. Y.H. Farzin (2000) provides some diretion here. http://papers.ssrn.com/sol3/papers.cfm? ... _id=246686

[EnergySpin]

Guys lots of info and suggestions in this thread ....
Lets try and settle the issues here , cause we can really make a much better job than other people who might have vested interests.
1) Regarding my suggestion to turn this into a community project. Which is the instrument that we should use? I liked the idea about sourceforge.net but at the same time, politeness mandates that we should not shoot down PO.COM by moving this intitiative elsewhere. After all , it is this site that got us together. So if our moderators can help us with formated displays and graphs we should continue posting here. Source code will have to be distributed somehow ; if this is not feasible through this web site, then by all means lets open a sourceforge project but we should be crossposting here as well. In addition maybe WHT could use his blog to cross post and TF_U use peakoil.nl to post PDF's as they are produced. This would ensure that the project attains the highest possible visibility.
2) Presentation of results : This is contigent upon a) the ability of our hosts to display graphical information and images and XML code. I have no way of posting in my department's web or ftp site and have IMG links pointing to those images. If someone else has this ability or maintains a blog, we could post there and cross link here, but it might also be easy to directly upload images. However this is a site administration issue so if Aaron or one of the other admins could let us know that would be great!!!!
If formulas have to be given we could use MathML (http://www.w3.org/Math/) ; Firefox directly presents equations written in MathML but IE needs a plugin like MathPlayer (available for free from Design Science : http://www.dessci.com/en/products/mathplayer/) . I could do all the rendering in MathML via Mathematica , but I have to know whether code posted in XML is rendered properly.
By the way there are many open source/free MathML WYSIWYG editors like MathCast (http://mathcast.sourceforge.net/home.html) so we are not limited to the big bad wolf from WRI.
Maybe one of the site administrators can answer the following question: can one post XML application code and have this displayed properly, or is this feature not implemented/disabled for security reasons?
4) Agenda for the community project. If we decide to go on with this, we should agree on what we try to accomplish. It is fairly obvious that the people who might be contributing are of different backgrounds, cultures-countries, have different political beliefs etc. It is important to realise that and try and mininize the potential of conflict by establishing and sticking to an agenda which deals with facts and predictions and nothing else. So I could be very happily co-exist with an Earth Firster and a Carbon Industry person in trying to estimate hydrocarbon production till they start to use the project to push a particular agenda. Using the project results is a different story though ... one is free to use them anyway he wants to, as long as he or she keeps the biases away while working on the project. Forgive the lenthy intro, but it is important to realise the truth in SilentE's statement found here:

Note to the unwary: under NO circumstances should you confuse friend-of-the-White-House Matt Simmons with LATOC-paranoid Matt Savinar.

So I propose to stick to the numbers and the numbers alone and reason only along those lines to avoid confusion between ontological and epistemological statements which have plagued most of the analyses of depletion and subsequent reasoning about implications/consequences/mitigation etc.
Having said all that , which number are we most interested at?
I believe (and this is open to discussion) that the quantities that we should try and estimate are the following:
a) Oil production in the future, peak date post depletion declines etc
b) Short term price and market fluctuations.
Note that both a) and b) are tightly interrelated and in fact influence each other. For if the market were to disappear overnight, depletion of the resource would stop, and post-peak the markets will berzerk.

Of course doing so will necessitate modeling of other quantities which affect the former and we should aim to find those individual quantities , understand their influence , put it in numbers and continuously update the models as time ticks by.
This brings us to the next issue:
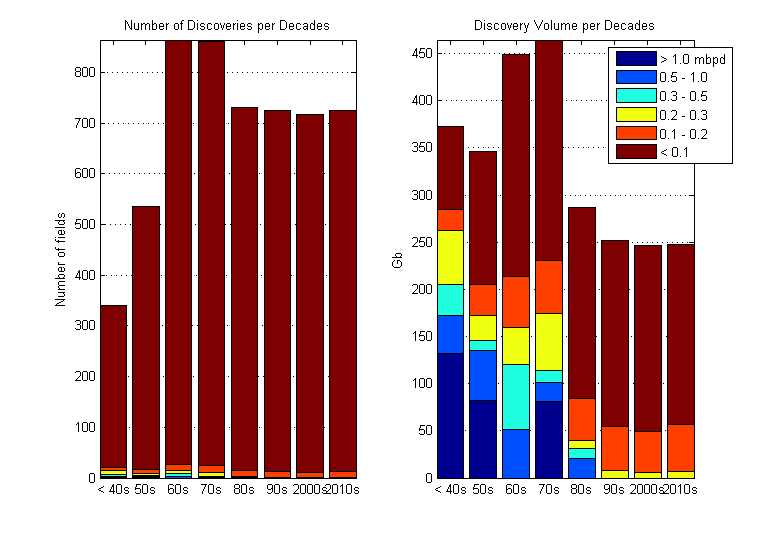
3) Methodology. I have noticed various attempts to model depletion in various journals (and by the way , most librarians think that I'm crazy when they realize that a MD is poking into the geology section of the library ). Most of the attempts tried to use fixed parametric forms for the description of the physical basis of the depletion suggested by theories based on Lotka-Volterra dynamics or Roper's mineral resource depletion theory: http://arts.bev.net/RoperLDavid/minerals/DepletTh.htm
I acknowledge WHT's reservations and wholeheartedly agree with him: They are useful default approximations and nothing else. I base my valuation on the following grounds:
a) they fail to take into account the physical reality of oil drilling- mining
b) they fail to take into account societal feedbacks that can either accelerate or attenuate the rate of depletion
c) they fail to take into account switching-time dynamics and non-linear phenomena
d) provide absolutely no way of incorporating technological advantages and/or assess their impact on dynamics of discovery, depletion, resource substitution (if and when present) etc.
e) provide no clear separation between the processes of discovery, depletion and markets
f) offer limited facilities for learning from data, or incorporating (imprecise) knowledge if it is known to exist about specific parameters

For example if one examines the following statement from Ropper's site:

At intermediate times there are no rational arguments that we can muster for any particular functional form for P(t) as a function of Q(t). So we shall consider several possibilities and let the production data for a given mineral “choose” which of the possibilities works best by performing least-squares fits to the data. Some obvious statements can be made, however: After rising slowly at earliest times, the production rate should begin to accelerate, then later (at an inflection point) decelerate until the production rate peaks at some time. Then the rate will begin to decline in a similar, but not necessarily symmetrical, fashion. Finally, P(t) will asymptotically approach zero. The simplest assumption that one could make which yields this kind of behavior is that P(t) is strictly proportional to the first power of both [Q¥-Q(t)] and Q(t) at all times;

I cannot see why it is obvious that such a sharp peak should exist and why URR is treated as a fixed quantity not only known in advance, but able to influence the depletion rate! (I will come to this latter - cause this is a crucial point)

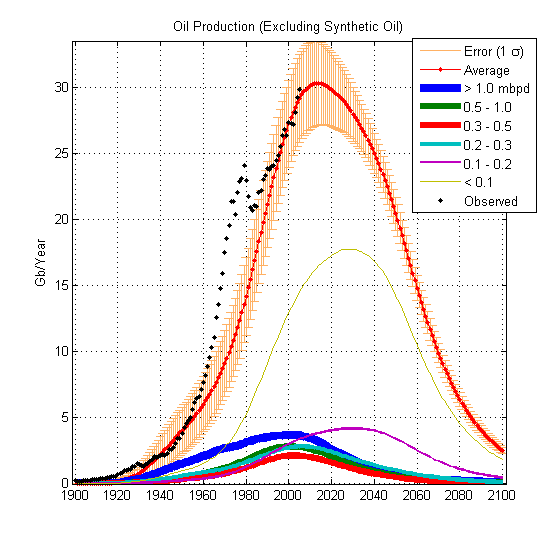
The mathematical constraints put on the production/depletion curve are way too restrictive. In reality the only thing we know about the production curve is that it starts from zero and ends up back to zero. This by virtue of the Roll's Theorem guarantees that the curve has at least one point where its derivative is zero (technically speaking one needs to transform time from [0,Infinity] to a finite interval i.e. [0,1] before one can apply Roll's theorem) . There could be more than one points with the same behaviour ... or more than one peaks, or even a plateau. However using such a curve is an oversimplification .... the production curve for the whole world will be given as a sum of many such curves ... each curve describing how a particular oil field is pumped in response to both geology and economy. And that sum, will also be way too complicated to conceptualize as a curve with a peak and an inflection point, even though it is too guaranteed to have at least one point where its derivative is zero (i.e. a maximum).

And yet many of the peak-oil modellers, use these approximations ... where as a more direct approach that took into account individual oil well data (when and where they exist) is more appropriate and more accurate.
Conceptually any approach that uses a single curve to fit the whole world implicitly assumes that either all oil fields are physically connected OR that the set of production curves describing the physical depletion of wells is closed under finite addition. But none of the curves usually presented in PO discussions satisfy this criterion i.e. the sum of two logistic curves is not a logistic curve, the sum of two gaussians is not a gaussian etc.
The fact that these methods worked beautfully for the lower US-48 (but guess what, Hubbert was wrong more than once about the URR of the US) , does not mean that they will work for the whole world. After all the political/societal/financial situations and geology in the US during the 20th century has probably little to do with the world as a whole.

What is the method I propose we should use (open to discussion) ?
It is a multi- step approach
A) Modelling of the physical processes that describe indivindual well behaviour. This models the geology in isolation of the economy!
We should aim to create simplified models of the way reservoirs empty when pumped and state them in mathematical terms. I do understand that modelling these structures in detail require complex CFD and structural geometries codes ... but at useful approximations can be ported from compartmental analysis and 0D electrical network modelling ). Compartmental analysis tries to model influx and outflux in a complex material system by decomposing it in a system of different compartments , with different volumes and connectivities. So for an example if the way an oil-well empties an "oil pocket" (I apologise for the use of inappropriate terms) behaves like a two compartmental system with one output to the outside world, then the resulting production curve will have a single peak provided the way the two compartment communicate does not change. The volumes of the compartments determine how much oil is potentially recoverable .... and therefore URR is a derived quantity that is related to the physical volumes of the compartments. There is actually quite a developed theory dealing with the identification of such systems i.e. estimating the number of compartments and their interactions from readings of the output of the compartment communicating with the real world. So for example one could use the theory and individual well data to answer questions like are advanced recovery methods allow us to increase the oil ultimately recoverable from a field (by "linking" hitherto unlinked compartments to the output compartment) OR do they simply change the relative volume of existing compartments and hence allow us to reach a high peak followed by a steep depletion? Of course it would quite a scientific hubris to suggest that this approximate method could substitute a detailed geologic simulation but it is better than nothing.

B) Modelling oil reservoir discovery = EXPLORATION. I found particularly enlightening the comments that rockdock made about log-normal distributions. Are these the terms "creaming curves" are understood? If we had access to discovery data we could estimate such distributions from start by using non-parametric kernel based methods and not rely on fixed parametric assumptions

C) Modelling the economy i.e. supply and demand . My understanding is that markets are modelled using Stochastic Differential Equations (e.g. Black Sholes formula), but I have absolutely no technical experience in either deploying these mathematical tools (although I'm a fast learner!) or even understand the econometrical context ... Any volunteers?

D) Modelling interactions: Actually the way economy interacts with geology is pretty straightforward in the compartmental framework. One increases the outflow rate constant (corresponding to opening up the pipes!) or decreases it in response to market signals. I have no way of knowing about exploration though ... conceptually I understand that high prices steer exploration but the argument is that exploration is now a dead end. What lied beneath the ground waiting to be discovered, has already been discovered. This will probably be difficult to answer .... any inputs from the geologists around here?

E) Learning the models : Quite an impressive number of unknown parameters have to be estimated, and the estimates refined as more production data are available. The only approach that may produce reasonable results is the probabilistic (or actually the Bayesian) approach .... known parameters are fixed, unknown parameters (or actually the probabilities describing their possible values) are estimated and Monte Carlo sims are run . They are the ones generating the scenarios!

F) Getting the data: rockdock/shakespear1/taskforce_unity any ideas?

4) Choice of tools : from the outset it is fairly obvious that we need software that is able to support the following mathematical methodologies:
a) various flavours of regression
b) probabilistic tools
For that I propose we use the open source R (http://www.R-project.org) and (win)BUGS from http://www.mrc-bsu.cam.ac.uk/bugs/welcome.shtml
The second can be dowloaded for free after registration .... and there is also a library that allows R and BUGS to communicate. This will at least guarantee a conformity of tools .... and allow people to test predictions/assumptions on their computers.
However such tools require data, data, data (old and new) and here I rest my case . I hope that other people may contribute ...

[rockdoc123]

Modelling oil reservoir discovery = EXPLORATION. I found particularly enlightening the comments that rockdock made about log-normal distributions. Are these the terms "creaming curves" are understood? If we had access to discovery data we could estimate such distributions from start by using non-parametric kernel based methods and not rely on fixed parametric assumptions

I currently have creaming curves (ie. size of discovery, date of discovery) for about 15 countries and I think they are relatively complete. I need to do some thinking about how I can get around the confidentiality issues etc. I think if as a group we agreed to have a statement that anything falling out of this study could not be used elsewhere and we kept the hard data relatively inaccessible it might be doeable but not sure. I have access to all of IHS, WoodMac and a few other sources not as well known.

)

Getting the data: rockdock/shakespear1/taskforce_unity any ideas?

as above. Actually maybe a good place to start is the UK North Sea database the DTI has. Laherre loves to cherry pick from this database to prove his point on EOR ineffectiveness but it is actually very, very complete...gives reserves, year discovery, production, injection etc. This is open to the public so it could avoid any confidentiality issues in the short term.

[EnergySpin]

I appreciate your take and expertise on data regression. But like Rockdoc, I have heartburn with the logistic model for more fundamental reasons. Why should it work at all for this class of behaviors? When did the strong non-linear component of the basic "predator/prey" get applied to oil depletion?

Thank you for your kind words ... I have been burnt with regressions (especially non-linear regressions) in the past so I tend to be very careful. My original criticism of the logistic/verhulst curves back in June/July was based on the numerical aspects of fitting such curves. I still do think that non-Bayesian NLR approaches are doomed to fail when applied to this family of curves. The geometry of the NLR space (as given by curvature measures of non-lineariyt) is such that estimators are going to be biased.
So if CC or Laherrere is using such approaches, they'd better delve into the technical aspects of non-linear regression .... they will be surprised to find out how one extra iteration of the algorithm can create vastly different pictures.
However I know think that there are additional reasons to "throw away" the logistic curve for the purpose of prediction (although it will surve an important role as a "default" model) and did write about it in my previous length post.
I strongly believe that one needs to take into account the physical reality of how a reservoir is drained and this why I suggested a tool called compartmental analysis as a model of reservoir drainage.

I was pleasantly suprised to notice that you are using a form of compartmental analysis without knowing it in your models
In the following post at your blog:
http://mobjectivist.blogspot.com/2005/0 ... model.html
you actually make some really good points about the shape of the depletion curve (we seem to agree that the mathematics constrain this curve to have at least one point where its derivative goes to zero i.e. a maximum and nothing else!), but I'm more interested in the following statement:

I use as an implicit assumption that any rate of extraction or flow is proportional to the amount available and nothing more; past and future history do not apply.

This is basically the equation for the output compartment in a multi-compartment system communicating with the real world. In actuality all the steps that you mention in your post try to model reality as fluxes of material between distrinct states, with rates proportional to the amount of material in different stages of the material flow graph.
For example if one has N compartments linked in a unidirectional chain graph, the output can be shown to be be given as the weighted sum of N exponential decay terms or go directly to ODE models that relate the constants to the physical properties of the systems (e.g. volumes of quantities, flux constants etc because under certain conditions of connectivity the two formulations are equivalent)

By extending this analysis into the reservoirs per se (e.g. each well => output compartment of a multi-compartment beneath the ground) one could try and ground the predictions to quantities that have a physical basis (and are potentially knowable from other non oil production sources). So for example computational modelling of the existing geologic structures could be used to put an upper limit of the recoverable oil from any reservoir , but then again I'm not a geologist so I do not know whether such data are routinely available, or whether one could have other measurements that might be of relevance and in the public domain

Stochasticity and the market signals (note I am not an econometrician , I hardly know if the term is accurate) could be represented as SDEs on the rate constants that describe the way materials flow in a multi-compartmental model of the physical process.
In such a case, one could use an ordinary differential equation (or more accurately a system of ODEs) model for the physical process of depletion and an SDE or a Hidden Markov model for transitions of the constants between different states in response to market signals etc.
IMHO it is important to decompose the model to physical processes and market/economy processes to avoid the pitfalls of previous analysis.
But all these are open to discussion ....

BTW does anyone know how CC or Laherrere estimate their curves? What are the parametric assumptions, numerical methodology etc? Just out of curiosity ....

[EnergySpin]

Modelling oil reservoir discovery = EXPLORATION. I found particularly enlightening the comments that rockdock made about log-normal distributions. Are these the terms "creaming curves" are understood? If we had access to discovery data we could estimate such distributions from start by using non-parametric kernel based methods and not rely on fixed parametric assumptions

I currently have creaming curves (ie. size of discovery, date of discovery) for about 15 countries and I think they are relatively complete. I need to do some thinking about how I can get around the confidentiality issues etc. I think if as a group we agreed to have a statement that anything falling out of this study could not be used elsewhere and we kept the hard data relatively inaccessible it might be doeable but not sure. I have access to all of IHS, WoodMac and a few other sources not as well known.

)

Getting the data: rockdock/shakespear1/taskforce_unity any ideas?

as above. Actually maybe a good place to start is the UK North Sea database the DTI has. Laherre loves to cherry pick from this database to prove his point on EOR ineffectiveness but it is actually very, very complete...gives reserves, year discovery, production, injection etc. This is open to the public so it could avoid any confidentiality issues in the short term.

I think we should approach this so as not to create problems for anyone (we are talking about copyrighted data here). I have the similar problem when I'm asked to test a new idea on legacy private gene expression datasets. This is why I start from open source datasets
Actually rockdock there are four sets of data that we need to consider:
A) Creaming curve data =>Exploration to date and the potential for future exploration
B) Individual field (or preferably well!!) production data and history of extraction methods applied to them
C) Information about projects coming on-line
D) Reservoir modelling data on different fields. Since I'm certainly using the wrong terms here, what I mean by this: reconstructions of the geologic structures that you guys operate on so we can test ideas on simplified models of the way the reservoir is drained.

Realistically what are the chances of getting public data on A-D?
Do we have such data for the US? (US might be a good test bed)
Is there a chance that a short not too technicai introduction (with lots of pictutes!!) on what does your garden variety oil field looks and operates like, exists on the web ? For example I do understand that a "source rock" is the source of the hydrocarbons we find in the reservoir (i.e. a potential space) that we empty, but what is the time scale relation between source rock-> reservoir AND reservoir->above the ground fluxes?
Go slowly on this one .... the only think I remember from geology is the technonic plates . But feel free to use terms from physical chemistry ... one of my current research projects involves diffusion differential equations (of molecules inside cells )

[rockdoc123]

A) Creaming curve data =>Exploration to date and the potential for future exploration
B) Individual field (or preferably well!!) production data and history of extraction methods applied to them
C) Information about projects coming on-line
D) Reservoir modelling data on different fields. Since I'm certainly using the wrong terms here, what I mean by this: reconstructions of the geologic structures that you guys operate on so we can test ideas on simplified models of the way the reservoir is drained.

Realistically what are the chances of getting public data on A-D?

A) is possible for certain places...the UK dataset I spoke of is a good one. I think Alaska BLM has a fair bit of data as well. There are also odd scattered papers in AAPG bulletin, CSPG bulletin, Journal Petroleum Geology and a few others that list discovery dates, sizes etc.....would require a fair bit of digging I think.
B) as above but good data will be fairly limited.....that's why IHS and WoodMac charge an arm and a leg to assemble it from the host governments.
C) Alexanders Gas and Oil is a good one and I believe it is more or less free. Oil and Gas International is without a doubt the best online source but costs poco dinero. If you go to Americanoilman.com there are a huge number of links listed...some news sites carry a fair bit on this info.
D) only places I have seen anything on reservoir modelling is AAPG bulletin, occassionally CSPG bulletin, SPE.

Do we have such data for the US? (US might be a good test bed)

The data is there, it's just that it ain't free...goddamn American capitalists!!

Is there a chance that a short not too technicai introduction (with lots of pictutes!!) on what does your garden variety oil field looks and operates like, exists on the web ? For example I do understand that a "source rock" is the source of the hydrocarbons we find in the reservoir (i.e. a potential space) that we empty, but what is the time scale relation between source rock-> reservoir AND reservoir->above the ground fluxes?

let me do a bit of hunting....new stuff just about everyday. The web has sure changed since I first started using it on Unix in the early nineties.

[khebab]

Statistical model for the distribution of field size:

In order to have a distribution of the oil field sizes, I checked the validity of lognormal model:


Figure 9

The blue points are Simmons data for the 6 oil field categories he defined (see Figure 8 ). The estimated sigma value is 4.2 when oil production is expressed in thousands of barrels per day. The fit is rather good.

Statistical model for the genration of random discovery data:

As discussed before, I'm missing a pdf for the small field discoveries. So I took the pdf of next category (Cat. 5) and rescaled it by the expected total numbers of discovery for small fields (4,000 up to the year 2000).

The algorithm to generate random discovery data is the following (this process is repeated N times):

Code: Select all

N= total number of oil fields
D= random variable associated to the decade of the discovery (we cosnider 8 decades from the 40s to 2010s).
Category= random variable associated with the field size (from supergiants (Cat. 1) to small fields (Cat. 6)).
P= random variable associated with the mean daily production output of an oil field (in thousands of barrels per day).

1) Randomly choose a decade d according to the following distribution:

prob(D) = [0.0623    0.0970    0.1577    0.1572    0.1317    0.1314    0.1314    0.1314]

2) According to the value of D=d, randomly choose a field category:

prob(Category | D= d) =[
    0.0057    0.0018         0    0.0011         0         0         0         0
    0.0057    0.0055    0.0034    0.0011    0.0014         0         0         0
    0.0086    0.0018    0.0068    0.0011    0.0014         0         0         0
    0.0230    0.0074    0.0068    0.0103    0.0014    0.0014    0.0014    0.0014
    0.0144    0.0148    0.0148    0.0148    0.0150    0.0150    0.0150    0.0150
    0.9425    0.9686    0.9682    0.9715    0.9810    0.9836    0.9836    0.9836]

2) According to the value of D=d and Category= c, randomly choose a field production output:

prob(P= p | D= d, Category= c)= ModifiedLognormal(p|sigma)

3) Derive an URR from the value of p:

beta ~ Unform([50, 110[)
URR= beta x p / (365x1e6)


Remarks:
- The first decade (40s) is in fact covering the period 1900-1940.
- The last step (3) has to be more justified because I don't know how to relates a field average production output and its URR.

The function called ModifiedLognormal() is a resampling of the original learn lognormal distribution on Figure 1 (a technique called importance sampling I believe). This technique produces a modified lognormal distribution based on the different pattern of discoveries observed for each decades.

Code: Select all

According to the value c of the realization of the random variable Category | D (ranging from 1 to 6) we do the following:

ModifiedLognormal:
  1) beta ~ Uniform([minp(c) maxp(c)[)
  2) We find the production p such as:
    LogNormalCDF(p) >= beta

[minp(c) maxp(c)[ is the production interval defined for the category c. For instance, if c= 2 we have [minp(c) maxp(c)[= [500 1,000[ tbpd.


Results:

Here are the results from a small simulation from 40 runs with N= 5,500 fields.


Figure 10

Figure 11

Figure 12

We can see that small fields have a large contribution The average peak position is:

2013.95 +/- 2 years at 30.55 +/ 1.0 Gb

URR= 2.664 +/- 0.11 Tb


Figure 13

Conclusions:

1. This an optimistic scenario because I repeated the discovery pattern from the 90s to the following decades (2000s and 2010s). Clearly, it's not obvious that we will have the same pattern.
2. A quick simulation seems to replicate expected proportions between the different field categories (supergiants and small fields produced 20% and 53% respectively of the world total production in 2000). There is a peak for small fields production only in 2030 as well as for Cat. 5 fields. Maybe this kind of fields are being overlooked.
3. the statistical relationship between a field mean production and its URR is not trivial.
4. The choice of the number N of oil fields influence greatly the result.
5. The statistical model to simulate worldwide discoveries (Figure 10) seems to replicate well the data from Simmons (Figure 8 ).